Modaliteit met Grafen
De (modale) logische achtergrond van ons concept wordt verwoord door Johan van Benthem:
(...)
M, s ⊨ □ Ø iff for all t with Rst, M, t ⊨ Ø ” (van Benthem, IEP)
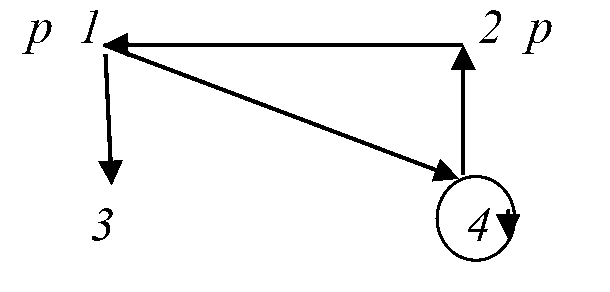
Gebruikmakend van de bovenstaande waarheidsdefinitie, de formule ◊□◊p is waar voor 1,4 maar is vals voor 2,3.
Verder zal ik de operator ◊ voor mogelijkheid niet langer gebruiken, aangezien voor de voorgestelde toepassing, namelijk voor visualisatie van causaliteit door gestructureerde gerichte analytische grafen, alleen noodzaaklijkheid nodig is. Maar eerst moeten we het probleem oplossen dat causaliteit met zich meebrengt bij het toepassen van de materiële implicaties van de formele logica, zoals axiomatiseerd door Frege en Hilbert. Een causale implicatie impliceert een logische implicatie, maar niet andersom.
(p □→ q) →(p → q)
Er zijn geen regels in de formele logica om te bepalen of een bepaalde oorzaak relevant is voor een bepaald gevolg, noch is er een regel die een reële relatie tussen oorzaak en gevolg vereist. Daarom zal ik vertrouwen op de Why-Because-Analysis (WBA) zoals voorgesteld door de incidentie onderzoekers aan de Universiteit van Bielefeld, voortbouwend op counterfactuals geïnitieerd door David Lewis (Ladkin, 2018, p. 2-5). Het formalisme van WBA maakt het mogelijk om de relatieve volledigheid, objectiviteit, falsifieerbaarheid en reproduceerbaarheid van de analyseresultaten zoveel mogelijk te garanderen. Het resultaat van de WBA is een Waarom-Omdat-Graaf (WBG). Wiskundig gezien is een WBG een gerichte, acyclische graaf. De knooppunten van de WBG vertegenwoordigen causale factoren van een incident. De gerichte pijlen vertegenwoordigen oorzaak-gevolgrelaties tussen de factoren. Tim Schürmann definieert de Counterfactual Test als volgt:
Deze Counterfactual Test voldoet aan de eisen die Alexander Stephanov in 1985 als “condition sine qua non” heeft gedefinieerd (Stephanov, 1985). Hij had die nodig om het gebruik van objecten in C++ te definiëren, waarvan de bibliotheken door hem werden geschreven. Ik zal ook definities van een bepaalde tijd en een bepaalde locatie introduceren, omdat ik niet alleen incidenten zal visualiseren, maar vooral statussen en processen op een bepaalde tijd en plaats, die zelfs op een andere bepaalde tijd en plaats kunnen worden herhaald, maar nog steeds kunnen worden toegeschreven aan dezelfde echte wereld.
Gestructureerde gerichte analytische grafen (SDAG) worden in dit concept gebruikt als wiskunde zonder getallen. Dit betekent niet dat het niet met getallen kan worden gebruikt. In verschillende onderzoeksdomeinen worden gewogen gerichte grafen gebruikt als analysemethode van datasets op zoek naar causale relaties, ‘causal discovery’ (Runge,2019). De causale relaties die in dit concept worden weergegeven, zijn echter gebaseerd op bewezen wetenschappelijke kennis. De grafen zelf zijn geen bewijs, maar een hulpmiddel om bewijzen verkregen op basis van logisch en wiskundig bewijs, te presenteren. De geformuleerde voorwaarden zullen uiteraard ook wiskundige uitdrukkingen zijn, maar ze zullen worden ingesloten in ‘Prolog’-termen. Deze moeten worden gezien als een oefening in formalisering, maar ze kunnen ook worden gebruikt om een formele database van regels en uitdrukkingen op te bouwen.
In ons concept van causaliteit gaan we uit van feiten en feitelijke toestanden. Feiten en toestanden worden structureel gelijk benaderd, maar zijn inhoudelijk verschillend. Toestand wordt in dit concept gebruikt als een meetbare en/of observeerbare categorie van feiten die onderdeel zijn van dezelfde verzameling van gebeurtenissen. Een voorbeeld: regenbui, sneeuw, motregen, hagel zijn onderdeel van de zelfde verzameling neerslag. Aangezien neerslag observeerbaar en meetbaar is, kan het als overkoepelende categorie conditioneel benaderd worden. Toestanden hebben gemeenschappelijke eigenschappen waarvan de drempels meetbaar en/of observeerbaar zijn. Bij de overgang van de ene naar de andere toestand is een proces de oorzaak van een overschrijding van minstens een van die drempels. De duur van dat proces kan een miliseconde zijn, maar bijvoorbeeld bij de vorming van regenwolken ook negen dagen. Het duurt gemiddeld negen dagen voor er regen uitvalt. In een histroische context kunnen die processen jaren en eeuwen in beslag nemen. Bij een specifiek alleenstaand feit kan men veel uitvoeriger onderzoeken waarom dat specifiek feit zich voordeed.
De modale logica heeft ondertussen aangetoond dat causaliteit perfect kan voorgesteld worden met gerichte acyclische grafen (van Benthem,IEP). Er wordt alleen nog gediscusieerd of die causaliteit nu invariant is of contextueel is. David Lewis koos voor invariantie. Ik kan daar mee leven op drie voorwaarden (1) dat men bij de analyse ook altijd de context analyseert, en nagaat of een regel algemeen blijft in alle contexten, indien niet moet men opsplitsen, (2) dat men moet aanvaarden dat de contexten in die mate kunnen veranderen dat men ook de regels moet veranderen en (3) een analyse moet ook altijd de histrorie en evolutie van een fenomeen analyseren. Die voorwaarden zijn tijdens de analyse van de klimaatverandering voldoende duidelijk geworden. In feite werden daar alle metereologische, hydrologische en ecologische systemen door elkaar gehaald zodanig dat opstellen van regels telkens opnieuw moest bekeken worden. Bij volstrekt nieuwe fenomenen komt dat regelmatig voor In de periode van covid19 moest men uiteindelijk ook de regel verwerpen dat het virus enkel verspreid werd met druppeltjes, het zat wel degelijk ook in de aerosols.
[terug naar begin pagina]Declaraties Gestructrureerde Gerichte Analytische Grafen
Omdat de pijlen van de graaf de volgorde van oorzaak en gevolg bepalen, is het niet nodig om getallen te gebruiken. Ook is het proces vastgezet tussen oorzaak en gevolg, de volgorde van processen heeft dus ook geen getallen nodig. De elementaire vorm van de voorgestelde gestructureerde gerichte analytische graaf (SDAG) is dus:
start_definition /= end_definition. Tautologie wordt uitgesloten
Een concrete wereld voorbeeld: Afkalven Noordpool ijskap
Een ketting van processen waar een end_status de start_status is voor een ander proces heeft de vorm:
start_definition /= end_definition /= chained_definition. Tautologie wordt uitgesloten. Deze ketting kan natuurlijk ook nog meer schakels bevatten
Een concrete wereld voorbeeld: Transpiratie Planten
Een exclusieve disjunctiie van processen, XOR heeft als form:
end_definition /= xor_definition. Het verschil tussen beide definities is de reden waarom ze elkaar uitsluiten
Net zoals in de formele logica kunnnen ook meerdere processen elkaal uitsluiten.
Een concrete wereld voorbeeld: Regen of Sneeuw
Een conjunctie van processen AND heeft de vorm:
Zoals in de formele logica kunnen meer dan twee processen tot een zelfde effect leiden.
Een concrete wereld voorbeeld: Verdamping
Een aaneenschakeling van processen tussen start_status en end_status is toegelaten maar deze precessen moeten uiteindelijk wel volledig gedefinieerd worden zoals verder word aangegeven. Deze aanaanschakelinng heeft de vorm:
process(definition) /= concat_process(definition). Tautologie wordt uitgesloten
Een concrete wereld voorbeeld: Fotosynthese
Vergeleken met de incident analyse van WBA gebruik ik dezelfde grafen structuur, waarbij WBA verschillende grafische containers gebruikt, rechthoeken voor het incident en sub-incidenten, ellipsen en achthoeken voor de processen die met elkaar verbonden zijn maar uiteindelijk in een rechthoek eindigen. WBA gebruikt in elk knooppunt slechts één lijn beschrijving in natuurlijke taal. Tot nu toe gebruikte ik alleen rechthoeken, maar deze zullen worden uitgebreid naar tabellen met meer regels en die dus de gestructureerde definities van de knooppunten bevatten. Op deze manier wordt het concept van WBA gewijzigd of, laten we zeggen, aangepast.
status(type): {
<thead> = prolog(status_expression) & <tbody> = prolog(condition) &
prolog(condition)…}
Prolog(expression) wordt als volg gediginieerd:
prolog(status_expression): {
element_name, element_quality, element_specification, T|P }
We definieren T:
T : time specification.
Dan definieren we P:
P : place specification.
Definities van tijd specificaties en plaats specificaties:
time specification: {time range | time description | time moment}
place specification: {specific place| other defined place}
Nu worden de condities gedefineerd:
prolog(condition) : {result of measurement | result of observation}
Voor processen gebruik ik de container process(type).
process(type): {
<thead> = prolog(process_description) & <tbody>= prolog(process_condition) &
prolog(process_condition)…}
Maar voor processen is de prolog(process_condition) optioneel, tenzij deze niet wordt gedefinieerd door een voorafgaande en volgende status(type), waarbij het verschil, met andere woorden, de werking van het proces normaal gesproken goed moet worden gedefinieerd in de definitie en de voorwaarden van start_status en end_status. Als er specifieke procesvoorwaarden zijn voor het initiëren en voortzetten van een proces, moeten deze voorwaarden ook opgelijst worden.
Voor gebruik en toepassing op een digitaal platform Scalable Vector Graphics (SVG) is gekozen voor een op XML gebaseerd vector beeldformaat voor het definiëren van tweedimensionale afbeeldingen. Hoewel SVG al in 2008 voor het eerst door WC3 werd gedefinieerd en de tweede versie uit 2011 dateert (Dahlström et al., 2011) is het minder bekend bij het publiek. Je kan bijvoorbeeld geen SVG uploaden op sociale media of blogs. Maar deze SVG is zeer krachtig, het kan ook hyperlinks bevatten en verwerken die betrekking hebben op tekstueel bewijs of context of een mix van tekstuele contexten en andere grafische elementen, wat verplicht is als gewerkt wordt op een digitaal platform.
Het gebruik van tabellen in grafen ziet er algemeen als volgt uit:
[terug naar begin pagina]Empirische Verificatie en Ingebedde Bronnen
Een sdag(type) moet minimaal één xlink:href-verwijzing bevatten naar een extern document dat het bewijs van het causale verband beschrijft. De xlink:href moet bewijsinformatie aanbrengen. Dit kan extern worden aangeleverd in tekstueel formaat of een combinatie van tekstueel en grafisch formaat. Dit kan worden gecodeerd als een HTML-link met het <rel> attribuut:rel="external" of rel="search.De bron van dit tekstueel materiaal moet gecertificeerd zijn komende van een encyclopedie (bvb de Wikipedia), komende van een wetenschappelijk instituut (bvb het ESA klimaatbureau) of aangemaakt zijn door een docent/leraar. Een “measurement system analysis” is de meest strikte vorm van certificering.
Wat als bewijs kan gebruikt worden, wordt bepaald door de internationale gemeenschap van wetenschappers. Waar en wanneer het bewijs geldig is wordt ook door die internationale gemeenschap bepaald. Maar die wetenschappers zijn wel enkel bevoegd in het domein waarover ze autoriteit beschikken.
Het volstaat dus niet dat een wiskundig logisch bewijs, consistent en goed geformuleerd is. Dit bewijs kan om verschillende redenen tekort schieten: (1) onvolledigheid; (2) niet relevant (3) gebaseerd zijnde op foute waarnemingen of niet herhaalbare experimenten, enzovoort. Het is dus aan de internationale gemeenschap van wetenschappers om uit te maken of een bewijs geldt en wel voldoende is.
Het wordt ingewikkeld als verschillende domeinen betrokken zijn bij een probleemstelling , zoals bij de klimaatverandering. Dit probleem wordt echter opgelost door internationaal overleg en internationale bijeenkomsten, waar een panel dan een interdisciplinair synthese rapport opstelt, zoals het IPCC deed in 2023.
[terug naar begin pagina]Referenties
Dahlström, Erik et al, (2011) Scalable Vector Graphics (SVG) 1.1 (Second Edition), W3C Recommendation 16 August 2011, <https://www.w3.org/TR/2011/REC-SVG11-20110816/>
Ladkin, Bernard (2018), Causal Analysis of Incidents with Why-Because Analysis using the SERAS® , Software Toolkit, CAUSALIS Ingenieurgesellschaft mbH, 2008, revised 2018-02-14, <https://rvs-bi.de/research/WBA/WBA-NewIntro20180214.pdf>
Lewis, David, (2004). “Causation as Influence” (expanded version), in Collins, Hall, and Paul 2004, 75–106, <https://www.andrewmbailey.com/dkl/Causation_As_Influence_long.pdf>
Menzies, Peter, (2019), Counterfactual Theories of Causation, 29 October 2019, Stanford Encyclopedia of Pholosophy, <https://plato.stanford.edu/entries/causation-counterfactual/>
Reed, Stephen K. (2012). Cognition : theories and applications. Wadsworth, Cengage Learning, 12 April 2012, ISBN 978-1-133-49228-3. OCLC 1040947645, <https://www.worldcat.org/nl/title/1040947645>
Runge, Jakob, et al. , (2019), Detecting and quantifying causal associations in large non-linear time series datasets. Sci. Adv.5,eaau4996 (2019). DOI: <https://www.science.org/doi/10.1126/sciadv.aau4996>
Schürmann, Tim, (WBA) 'Counterfactual Test’, Workgroup RVS, Faculty of Technology, Bielefeld University) <https://rvs-bi.de/research/WBA/IntroWBA-ENG.pdf>
Stepanov, Alexander (1985), Towards a Theory of Causal Implication, Department of Electrical Engineering and Computer Science, Polytechnic University of New York, 1985, <http://stepanovpapers.com/TOWARDS%20A%20THEORY%20OF%20CAUSAL%20IMPLICATION.pdf >
van Benthem, Johan, (IEP), Modal Logic: A Contemporary View, University of Amsterdam, Stanford University, and Tsinghua University, The Netherlands, U. S. A., and China, <https://iep.utm.edu/modal-lo/>
Weatherson, Brian, "David Lewis", (2021)The Stanford Encyclopedia of Philosophy (Winter 2021 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/win2021/entries/david-lewis/>.
[terug naar begin pagina]