Visualisation of causality and sequential action

Introduction

The use of directed graphs as a visualisation of scientific evidence is not new; there are countless applications for this. For example, in biology, anthropology, medical sciences and accident analysis. In various research domains, weighted directed graphs are used as a method for analysing datasets in search of causal relationships, or 'causal discovery' (Runge, 2019).

A proposal to link causal discovery to an ontology can be found in "Reasoning about Causal Relationships: Inferences on Causal Networks". The problem with this automatic link is that it is often ambiguous (Rotman, Heisty, 2013). This problem can be avoided here because the linking of factual data to conclusions is not entrusted to an algorithm with stochastic variables, but is based on a logically provable scheme created by people who know the subject matter, researchers, teachers and other experts, who can justify their choices on the basis of scientific consensus.

Triplets for Causation & Sequential Action

EDAG points to Elucidative Directed Analytic Graphs.

The general structure of EDAG is: measurable state -> process -> measurable state. When confronted with complex processes: measurable state -> process -> process -> process -> measurable state.

The measurements must be relevant and be able to serve as a scientifically accepted measure of the causal relationship or relationship between direct successive sequential actions. The origin of the measurements and the storage of the data of the measurements must be publicly available and transparent accesible for everybody.

New in this application is the detailed and explicit use of Scallar Vector Graphs (SVG) that gives the possibility to
(1) integrate images and text fluently,
(2) integrate images in images, admitting meaningful diagrams.
(3) One can retrieve the images, save and scale etc.
(4) From each node and arrow, a Uniform Resource Locator (URL) can point to an explanatory text.
(5) That way, you turn your SVG into a semantic database of texts and images.
(6) An SVG can also be embedded in the explanatory text, allowing you to create a layered explanation system.
(7) The latter offers the opportunity to take an interdisciplinary approach to a problem.

The elements of a directed graph are minimal to nodes, connected by directed arrow. The most straightforward application is to connect two objects, facts, states (the nodes) with a causal process (the arrow). This is called a causal triplet.

Each node consists at least of two parts: (1) a header identifying an object, fact status or process (2) The formulation of the condition(s) underlying the occurrence of this specific fact, state, or process. These conditions must always be the result of measurements, observations, or both.

Modal Logics of the EDAG concept

De causal relations that are visualised in this concept, are based on knowledge that has been proven and accepted by the science community. The graphs are not a proof but a tool to visualise proofs. The concept can only be used for discrete processes. The transition from one state to another should be measurable and at least one threshold should be measurable that explains the transition from one state to another.

Prolog expressions are used to represent all parts of the graph.

In addition to the predicates used to formulate conditions, seven predicates are also used structurally for standard functions: proc/2 for processes, stat/2 for states, img/2 for bitmap images, url/2 for URLs to external clarification and references, label/1 for the label of the graph and the timescale, exor/2 for the exclusive disjunction, and ltext/2 to generate plain text, as in the example below.

ltext("The water vapour clumps together around microscopic particles in the air, such as dust or salt crystals, which serve as condensation nuclei.").

The space for clarification using ltext/1 are limited. However, scientifically supported evidence with references can be consulted via the URLs in the graph.

The sequence in a process is represented by ordinal natural numbers. The number of the consequence object must always be greater than the number of the original object (before the cause had an effect). The same numbers are used for the expressions of the conditions as references to the respective objects. For processes, the second term is a list of numbers that refers to the start and end status of that process. See example below.

In the nodes of the graph, you'll find the definitions of the initial and final states, and the definition of the process is shown near the arrows. Below the definitions of the initial and final states, the conditions for reaching that state are listed. The principle of the "conditio sine qua non" is used here.

The given conditions defining a fact or state must always be true at the same time. Thus they are connected with the “AND” operator. In the node they are hold together by a table.

To ensure consistency, the production of the EDAG graphs is linked to a logical proof in Prolog via unification. These declarations in turn can serve as a consultable semantic database (Wielemaker,2005). The sDAG parser in Java checks extra for tautology. Prolog is based on Horn clauses and backtracking, depth-first search.

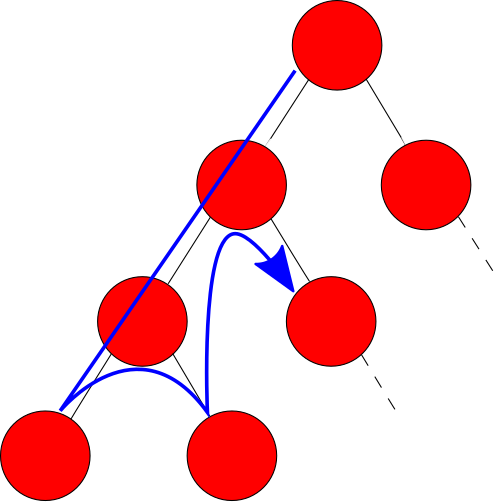
Points of interest

(1) Unlike in formal logic, in modal logic there is an additional dependent relation between cause and effect, the 'conterfactual dependence'. If y is counterfactually dependent on x and z is counterfactually dependent on y, but z is not also counterfactually dependent on x, then there is no transitivity. If this is the case, we call it sequential action.

Transitivity in Formal Logic
whenever (x → y) and (y → z) then also (x → z)
No transitivity in causality of Modal Logic
whenever (x □→ y) and (y □→ z) then not automaticely (x □→ z)

Sequential action is not represented by a directed solid line but by a directed dotted line to indicate the difference with causality.

(2) Embedding an SVG image in a node is possible, but if that SVG also contains an image, the browser won't see it. Besides that technical problem, there is also an epistemological argument not to do so. Between different scientific disciplines there is always an unruly zone where rules and terminology are incompatible. For example, while redundancy is seen as positive in ecology, redundancy in logic and information theory are to avoid. Ditto for metereology and climate science, between biology and sociology, and so on. This is due to different abstaction levels and different time scales. There is also absolutely no intention to abolish the disciplines, but rather to cooperate across the boundaries of the disciplines.

In a node you can link to an explanatory text file (HTML or XML) in which you can embed an EDAG graph. The advantage of that solution is that you can make clear what the connection is between the two logical layers and where the boundaries are for each logical layer. You wil find an example of such an imbedding in the upper node of this EDAG.

(3) Different approaches are also related to time scales of analysis. This applies not only across disciplines but also within disciplines themselves. A good indication of that time scale per graph is highly recommended.

(4) Graphs provide the basic schema of algorithms. They are therefore also an exercise in algorithmic thinking.

 
 
 
 
 
 

Consulted Resources

Alkharashi M. Comparing experiential versus conventional learning on knowledge retention for teaching surgery to medical graduates. Saudi J Ophthalmol. 2020 Dec 28;34(2):107-110. doi: 10.4103/1319-4534.305042. PMID: 33575531; PMCID: PMC7866721 <https://pmc.ncbi.nlm.nih.gov/articles/PMC7866721/>.

Beccuti, Francesco, 2024, Gödel and Turing on mathematical intuition: between Platonism and Embodiment, The Philosophy of Mathematics Education Journal, 42 (Dec. 2024), Università di Cagliari, <https://sites.exeter.ac.uk/pmej/wp-content/uploads/sites/569/2024/12/Beccuti-Godel-and-Turing-on-Mathematical-Intuition-XX.pdf>

Stefano R. Belli, Robert D. Rogers, Jennifer Y.F. Lau, Adult and adolescent social reciprocity: Experimental data from the Trust Game, Journal of Adolescence, Volume 35, Issue 5, 2012, Pages 1341-1349, ISSN 0140-1971, https://doi.org/10.1016/j.adolescence.2012.05.004. (https://www.sciencedirect.com/science/article/pii/S0140197112000814).

Berners-Lee, Tim, James Hendler, and Ora Lassila. The semantic Web. Scientific American, 284(5):34–43, May 2001.

Dahlström, Erik et al, (2011) Scalable Vector Graphics (SVG) 1.1 (Second Edition), W3C Recommendation 16 August 2011, <https://www.w3.org/TR/2011/REC-SVG11-20110816/>

Jawed S, Amin HU, Malik AS, Faye I. Classification of Visual and Non-visual Learners Using Electroencephalographic Alpha and Gamma Activities. Front Behav Neurosci. 2019 May 7;13:86. doi: 10.3389/fnbeh.2019.00086. PMID: 31133829; PMCID: PMC6513874. <https://pmc.ncbi.nlm.nih.gov/articles/PMC6513874/>

Ladkin, Bernard (2018), Causal Analysis of Incidents with Why-Because Analysis using the SERAS® , Software Toolkit, CAUSALIS Ingenieurgesellschaft mbH, 2008, revised 2018-02-14, <https://rvs-bi.de/research/WBA/WBA-NewIntro20180214.pdf>

Levonian, E. Auditory and visual retention in relation to arousal. AVCR 16, 57–62 (1968). https://doi.org/10.1007/BF02768681, <https://link.springer.com/article/10.1007/BF02768681>

Lewis, David, (2004), “Causation as Influence” (expanded version), in Collins, Hall, and Paul 2004, 75–106, <https://www.andrewmbailey.com/dkl/Causation_As_Influence_long.pdf>

Menzies, Peter, (2019), Counterfactual Theories of Causation, 29 October 2019, Stanford Encyclopedia of Pholosophy, <https://plato.stanford.edu/entries/causation-counterfactual/>

Jean Piaget, 1932-1985, Le jugement moral chez l’enfant, ISBN 2 13 039056 0, 6me édition 1985, Presse Universitaire de France, Paris.

Reed, Stephen K. (2012). Cognition : theories and applications. Wadsworth, Cengage Learning, 12 April 2012, ISBN 978-1-133-49228-3. OCLC 1040947645, <https://www.worldcat.org/nl/title/1040947645>

Roark CL, Lescht E, Hampton Wray A, Chandrasekaran B. Auditory and visual category learning in children and adults. Dev Psychol. 2023 May;59(5):963-975. doi: 10.1037/dev0001525. Epub 2023 Mar 2. PMID: 36862449; PMCID: PMC10164074.

Rottman BM, Hastie R. Reasoning about causal relationships: Inferences on causal networks. Psychol Bull. 2014 Jan;140(1):109-39. doi: 10.1037/a0031903. Epub 2013 Apr 1. PMID: 23544658; PMCID: PMC3988659. <https://pmc.ncbi.nlm.nih.gov/articles/PMC3988659/>.

Runge, Jakob, et al. , (2019), Detecting and quantifying causal associations in large non-linear time series datasets. Sci. Adv.5,eaau4996 (2019). DOI: <https://www.science.org/doi/10.1126/sciadv.aau4996>

Quinn C, Taylor JSH, Davis MH. Learning and retrieving holistic and componential visual-verbal associations in reading and object naming. Neuropsychologia. 2017 Apr;98:68-84. doi: 10.1016/j.neuropsychologia.2016.09.025. Epub 2016 Oct 6. PMID: 27720949; PMCID: PMC5407349.

Schürmann, Tim, (WBA) 'Counterfactual Test’, Workgroup RVS, Faculty of Technology, Bielefeld University) <https://rvs-bi.de/research/WBA/IntroWBA-ENG.pdf>

Stepanov, Alexander 1985), Towards a Theory of Causal Implication, Department of Electrical Engineering and Computer Science, Polytechnic University of New York, 1985, <http://stepanovpapers.com/TOWARDS%20A%20THEORY%20OF%20CAUSAL%20IMPLICATION.pdf >

Storbeck J, Clore GL. Affective Arousal as Information: How Affective Arousal Influences Judgments, Learning, and Memory. Soc Personal Psychol Compass. 2008 Sep 1;2(5):1824-1843. doi: 10.1111/j.1751-9004.2008.00138.x. PMID: 25067943; PMCID: PMC4110743. <https://pmc.ncbi.nlm.nih.gov/articles/PMC4110743/>.

van Benthem, Johan, (IEP), Modal Logic: A Contemporary View, University of Amsterdam, Stanford University, and Tsinghua University, The Netherlands, U. S. A., and China, <https://iep.utm.edu/modal-lo/>

Wouter van den Bos, Michiel Westenberg, Eric van Dijk, Eveline A. Crone, Development of trust and reciprocity in adolescence, Cognitive Development, Volume 25, Issue 1, 2010, Pages 90-102, ISSN 0885-2014, https://doi.org/10.1016/j.cogdev.2009.07.004. (https://www.sciencedirect.com/science/article/pii/S0885201409000616).

Wielemaker, J. (2005). An Optimised Semantic Web Query Language Implementation in Prolog. In: Gabbrielli, M., Gupta, G. (eds) Logic Programming. ICLP 2005. Lecture Notes in Computer Science, vol 3668. Springer, Berlin, Heidelberg. <https://doi.org/10.1007/11562931_12>

Zopf R, Giabbiconi CM, Gruber T, Müller MM. Attentional modulation of the human somatosensory evoked potential in a trial-by-trial spatial cueing and sustained spatial attention task measured with high density 128 channels EEG. Brain Res Cogn Brain Res. 2004 Aug;20(3):491-509. doi: 10.1016/j.cogbrainres.2004.02.014. PMID: 15268926. <https://pubmed.ncbi.nlm.nih.gov/15268926/>.

Attribution

Copyright © 2025 Verhoeven. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY).